CrIBo

Summary

We introduce a novel self-supervised learning (SSL) approach (CrIBo) tailored to enhance dense visual representation learning. To the best of our knowledge, CrIBo is the first end-to-end online SSL approach that explicitly enforces cross-image consistency at the object/object-part level.
CrIBo emerges as a notably strong and adequate candidate for in-context scene understanding tasks without compromising the performance on standard segmentation benchmarks.
CrIBo shows state-of-the-art performance on dense nearest neighbor retrieval task, compatible with scene-centric datasets, addressing a gap in the existing cross-image SSL literature.

Figure: Positioning of CriBO in the landscape of self-supervised learning. a) Illustration of the cross-image self-supervision concept. c) Depiction of object-level self-supervision. b) CrIBo benefits from both learning paradigms.

Method: CrIBo

Our method, CrIBo, is realized through the following steps:

Identify semantically coherent regions within the image to create object-level representations.
Match pairs of object-level representations across images.
Apply cross-image consistency between pairs of matching object-level representations.

Task Affinity Diagram — **Figure:** **High-level overview of cross-image object-level bootstrapping (CrIBo).** Given an encoder f and a pair of augmented views, described as x̃₁ and x̃₂, object representations *c_i^k* (depicted as colored object masks) from each view i are computed. Using a memory bank, the nearest neighbors of each object representation *c₁^k* from the first view are retrieved. A self-supervised consistency loss (depicted as colored arrows) is then enforced between *c₂^k* and its corresponding retrieved neighbor from the other view, *NN(c₁^k)*.

1. Semantically Coherent Image Regions

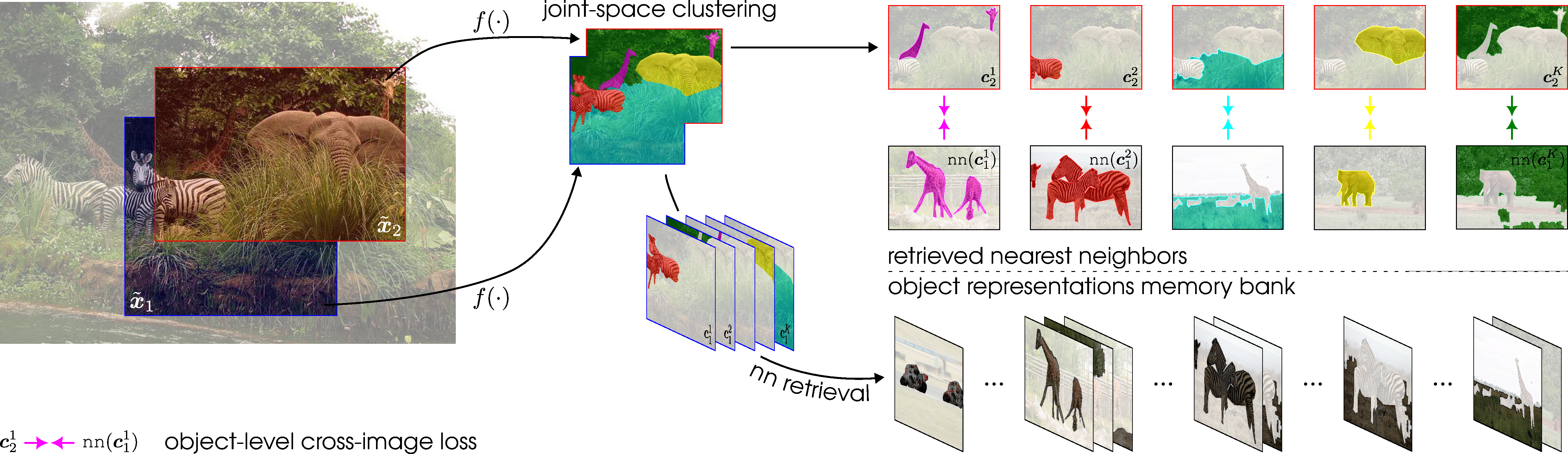
The first step towards cross-image object-level bootstrapping is to identify semantically coherent image regions within the images. To that end, we rely on an online joint-space clustering algorithm from [Stegmuller_2023_CVPR].

Joint-space clustering.

The clustering algorithm takes as input the dense representations \( \mathbf{z}_1 \in \mathbb{R}^{N \times d} \) and \( \mathbf{z}_2 \in \mathbb{R}^{N \times d} \) associated with the two augmented views and concatenates them along the token axis to obtain the dense representation of the joint-view, \( \mathbf{z}_{\text{cat}} \in \mathbb{R}^{2N \times d} \). The \( 2N \) tokens are subsequently partitioned into \( K \) clusters to produce semantically coherent and spatially compact clusters. A hyperparameter \( \lambda_{\text{pos}} \) modulates the importance of the spatiality against that of the semantic. The resulting assignment is encoded in a matrix \( \mathbf{Q}^{*} \in \mathbb{R}^{2N \times K} \), which can be split in two to obtain the view-wise assignments \( \mathbf{Q}^{*}_1, \mathbf{Q}^{*}_2 \in \mathbb{R}^{N \times K} \). Here \( \mathbf{Q}^{*}_i(n,k) \) denotes a soft-assignment of token \( n \) to object-cluster \( k \) in view \( i \). These can in turn be used to compute the \( K \) object representations \( \mathbf{c}_i \in \mathbb{R}^{d} \) in each view \( i \) as follows:

\[ \mathbf{c}_i^k = \sum_{n \in [N]} \mathbf{Q}^{*}_i(n,k) \cdot \mathbf{z}_i^n,\quad i \in \{1,2\} \]

Note that the columns of \( \mathbf{Q}^{*}_i \) undergo \( l_1 \) normalization, rendering the object representations as affine combinations of local representations. observed that the cross-view correspondence is provided for free as the object representation \( \mathbf{c}_1^k \) from the first view is matched to \( \mathbf{c}_2^k \) in the second one as a consequence of the joint-space clustering. In practice, it can be the case that some objects are exclusive to one of the two views, i.e., \( \sum_{n \in [N]} \mathbf{Q}^{*}_i(n,k) = 0 \). In that case, the object \( k \) is simply discarded from the view where it is present.

2. Cross-Image Object Matchings

In the section on semantically coherent image regions, we detail the methodology for identifying objects within the views of a given image and establish the strategy for their alignment from one view to another. Following this step is the critical phase of aligning such objects across images. We rely on a pair of memory banks \( \mathcal{M}_1 \) and \( \mathcal{M}_2 \), populated with object representations extracted from the first and second views during previous iterations. Thus, the memory banks \( \mathcal{M}_{i} \) can be queried with an object representation \( \mathbf{c}_i^k \) to retrieve its nearest neighbor:

\[ \text{NN}(\mathbf{c}_i^k, \mathcal{M}_i) \triangleq \underset{\mathbf{c} \in \mathcal{M}_i}{\arg\max} \frac{\mathbf{c}^\top \mathbf{c}_i^k}{\| \mathbf{c} \|_2 \| \mathbf{c}_i^k \|_2} \]

Here, we consider \( \text{NN}(\mathbf{c}^k_1, \mathcal{M}_{1}) \) and \( \mathbf{c}_1^k \) as cross-image object-level matches.

Cycle-consistent matchings.

Figure: Illustration of cycle-consistent matchings. Such matchings are invariant to data augmentations and reciprocal, loosely speaking.

At the beginning of the pretraining phase, when the encoder is randomly initialized, relying on the nearest neighbor operator to identify cross-image object-level matches is not well grounded. Indeed, this straightforward approach assumes that the representations of similar objects are close in the embedding space, an assumption that does not hold at the initialization. Therefore, enforcing consistency between such pairs of semantically distinct objects should be avoided. To that end, we design a semantic closeness condition, which is only fulfilled when the matches are established based on high-level features, thus enabling the discarding of invalid positive pairs that do not share a semantic similarity.

At a high level, we consider a pair of objects as a valid positive pair if they are the nearest neighbors of each other. In practice, the criterion is implemented as follows. Starting from an object representation \( \mathbf{c}_1^k \) in the batch of first views, its nearest neighbor \( \texttt{nn}(\mathbf{c}_1^k, \mathcal{M}_1) \) in the queue is found using the nearest neighbor operator. To ensure that the criterion is invariant to data augmentation, we then switch to the queue of second views via the \( \texttt{jump}(\cdot) \) operator:

\[ \texttt{jump}(\mathbf{c}_1^k) \triangleq \mathbf{c}_2^k, \quad \quad \texttt{jump}(\mathbf{c}_2^k) \triangleq \mathbf{c}_1^k \]

From this step, we obtain \( \texttt{jump}(\texttt{nn}(\mathbf{c}_1^k, \mathcal{M}_1)) \) and retrieve its NN in the batch of second views \( \texttt{nn}(\texttt{jump}(\texttt{NN}(\mathbf{c}_1^k, \mathcal{M}_1)), \mathcal{B}_{2}) \). The final step consists of switching back to the batch of first views and verifying if the resulting object is the same as the one we started from. More formally:

\[ \mathcal{O}(\mathbf{c}_i^k) \triangleq \begin{cases} true & \text{if} \quad \mathbf{c}_i^k = \texttt{jump}(\texttt{nn}(\texttt{jump}(\texttt{nn}(\mathbf{c}_i^k, \mathcal{M}_i)), \mathcal{B}_j))\\ false & \text{otherwise} \end{cases} \quad i, j \in \{1, 2\}, i \neq j \]

3. Self-Supervised Training Objectives

CrIBo’s final training objective involves three distinct types of self-supervision: cross-view object-level, cross-image object-level, and global cross-image. All levels of self-supervision are based on the self-distillation mechanism, which employs a student-teacher pair of siamese networks \(f_s\) and \(f_t\), respectively. Given two augmented views \(\tilde{\boldsymbol{x}}_1\) and \(\tilde{\boldsymbol{x}}_2\), global representations and object representations can be obtained for each view and each network within the siamese pair.

Cross-View Object-Level Self-Supervision

The object representations from the teacher and student are fed to their respective head \(h_s\) and \(h_t\) to output probability mass functions whose sharpness can be modulated via temperature parameters (\(\tau_{s}\) and \(\tau_{t}\)). For the teacher, this translates to:

\[ \mathbf{p}_{i,t}^k = \texttt{softmax}\left(\text{head}_{t}(\mathbf{c}_{i,t}^k) / \tau_{t} \right), \quad i \in \{1,2\} \]

The student's projections are obtained analogously. The cross-view object-level loss is expressed as the averaged cross-entropy over all pairs of object representations and making the loss symmetric with respect to the student/teacher:

\[ \mathcal{L}_{cv}^{o} = \frac{1}{K}\sum_{k \in [K]} \left( H(\mathbf{p}_{1,t}^k, \mathbf{p}_{2,s}^k) + H(\mathbf{p}_{2,t}^k, \mathbf{p}_{1,s}^k) \right) \]

where \(H(\mathbf{a}, \mathbf{b}) = -\sum_{l=1}^{L} \mathbf{a}_{l} \log (\mathbf{b}_{l})\) denotes the cross-entropy.

Cross-Image Object-Level Self-Supervision

Once all object representations in the batch have been retrieved, the cross-image object-level loss is enforced in a manner analogous to its cross-view counterpart. The nearest neighbors are first fed to the projection head as follows:

\[ \tilde{\mathbf{p}}_{i,t}^{k} = \texttt{softmax}\left(h_{t}(\texttt{nn}(\mathbf{c}_{i,t}^k)) / \tau_{t} \right), \quad i \in \{1,2\} \]

Note that these projections are only defined for the teacher since the \(\texttt{nn}(\cdot)\) operator is not differentiable. The formulation of the cross-image object-level loss aligns with that in the cross-view loss up to the filtering of invalid positive pairs:

\[ \mathcal{L}_{ci}^{o} = \frac{1}{Z_1}\sum_{k \in [K]} \mathbb{1}_{\{\mathcal{O}(\mathbf{c}_1^k)\}} H(\tilde{p}_{1,t}^{k}, p_{2,s}) + \frac{1}{Z_2}\sum_{k \in [K]} \mathbb{1}_{\{\mathcal{O}(\mathbf{c}_2^k)\}} H(\tilde{p}_{2,t}^{k}, p_{1,s}) \]

where \( \mathbb{1}_{\{\cdot\}} \) denotes the indicator function and where \( Z_1 \) and \( Z_2 \) are normalization constants, i.e., \( \sum_{k \in [K]} \mathbb{1}_{\{\mathcal{O}(\mathbf{c}_1^k)\}} \) and \( \sum_{k \in [K]} \mathbb{1}_{\{\mathcal{O}(\mathbf{c}_2^k)\}} \), respectively.

Global Cross-View Self-Supervision

Importantly, both the clustering and the bootstrapping steps are contingent on the quality of the representations. To avoid potential instabilities, we incorporate a global cross-view loss into our framework, offering meaningful self-supervision at any stage of the pretraining. This loss is analogous to the one from the cross-view object-level loss except that it is applied to the global representation (\(\mathbf{z}_{1,s}\), \(\mathbf{z}_{2,s}\), \(\mathbf{z}_{1,t}\), and \(\mathbf{z}_{2,t}\)), which are fed to a dedicated head \( \overline{h} \):

The global cross-view projections are defined as follows:

\[ \overline{p}_{i,t} = \texttt{softmax} \left(\overline{h}_{t}(\mathbf{z}_{i,t}) / \overline{\tau}_{t}\right), \quad i \in \{1,2\} \]

where \(\overline{\tau}_{s}\) and \(\overline{\tau}_{t}\) are the corresponding temperature parameters for the \(\overline{L}\)-dimensional output distribution. The global cross-view loss is defined as:

\[ \mathcal{L}_{cv}^{g} = H(\overline{p}_{1,t}, \overline{p}_{2,s}) + H(\overline{p}_{2,t}, \overline{p}_{1,s}) \]

where \(H(\mathbf{a}, \mathbf{b}) = -\sum_{l=1}^{\overline{L}} \mathbf{a}_{l} \log (\mathbf{b}_{l})\).

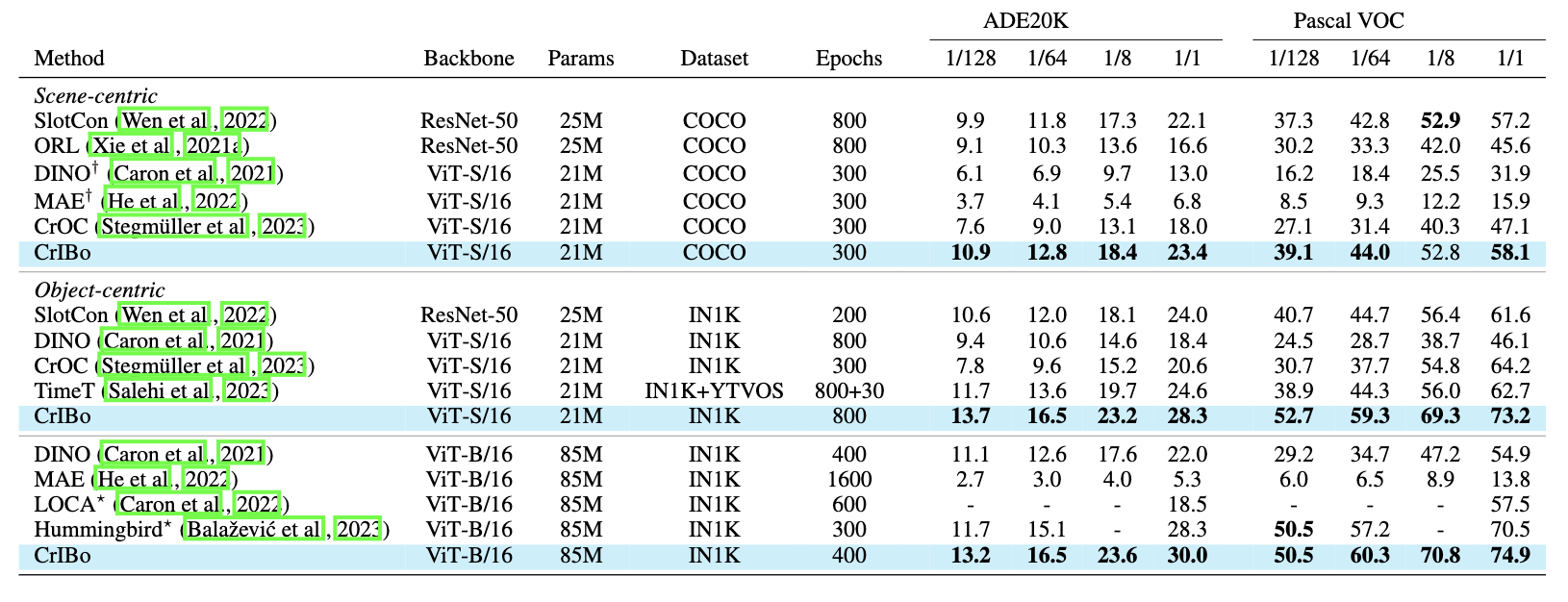
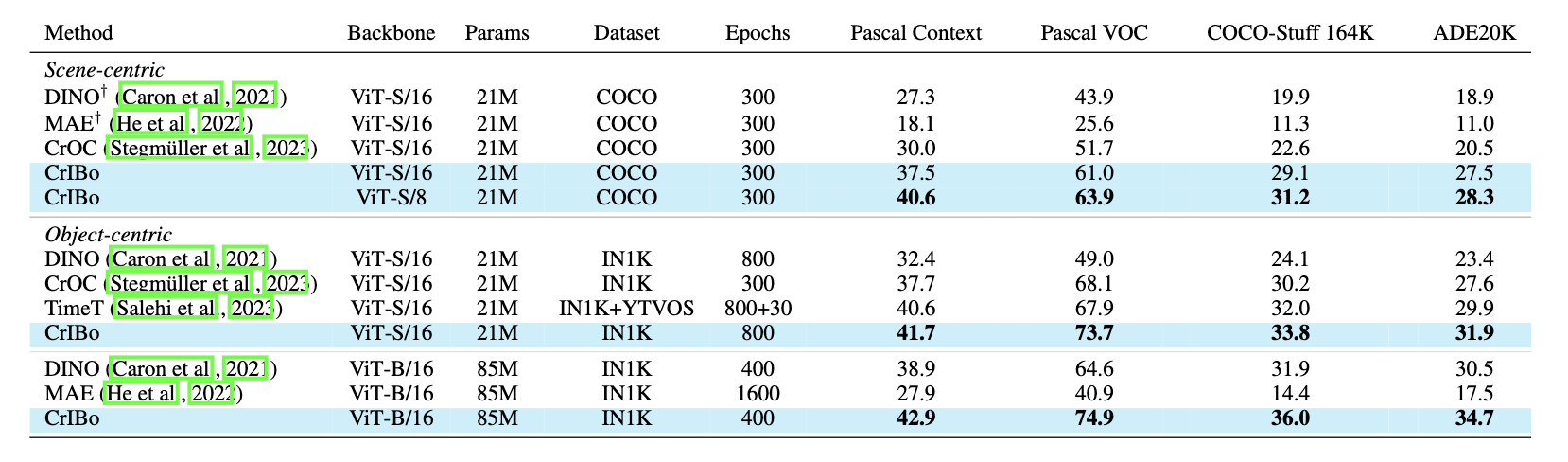
Finally, we obtain the overall training objective of CrIBo as a sum of its individual components:

\[ \mathcal{L}_{\text{tot}} = \mathcal{L}_{cv}^{g} + \mathcal{L}_{cv}^{o} + \mathcal{L}_{ci}^{o} \]

The student's parameters are optimized to minimize the above loss whereas the parameters of the teacher are updated via an exponential moving average of the student's weights.

Experimental Results

1. CrIBo shows state-of-the-art performance on dense nearest neighbor retrieval task

Figure: Dense nearest neighbor retrieval. The quality of the learned spatial features is probed with a k-NN classifier and using different ratios of training data. The depicted mIoU scores are derived from the validation sets of two scene-centric datasets. \( \dagger \) refers to our own reproduction from official GitHub repositories. If not specified, publicly available checkpoints are used. \( \star \) denotes results taken from [Balavzevic et al. (2023)].

2. CrIBo exhibits commendable performance in linear segmentation

Figure: Linear segmentation with frozen backbones. The linear decoder from [Segmenter] is trained on the frozen spatial features obtained with various self-supervised learning methods. We report the mIoU scores achieved on the validation sets of 4 different datasets. \( \dagger \) refers to our own reproduction from official GitHub repositories. If not specified, publicly available checkpoints are used.

3. CrIBo adeptly evolve into remarkable specialists

Figure: Finetuning evaluation with Segmenter. Backbones pre-trained with different self-supervised learning methods are finetuned using [Segmenter]. We report the mIoU scores achieved on the validation sets of 4 different datasets. \( \dagger \) refers to our own reproduction from official GitHub repositories. If not specified, publicly available checkpoints are used.

BibTeX

@inproceedings{Lebailly2024CrIBo,
  title={CrIBo: Self-Supervised Learning via Cross-Image Object-Level Bootstrapping},
  author={Lebailly, Tim and Stegm{\"u}ller, Thomas and Bozorgtabar, Behzad and Thiran, Jean-Philippe and Tuytelaars, Tinne},
  booktitle={The Twelfth International Conference on Learning Representations},
  year={2024}
    }

Acknowledgement

This website is adapted from Nerfies and LLaVA, licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

CrIBo : Self-Supervised Learning via Cross-Image Object-Level Bootstrapping

ICLR 2024 (Spotlight)

🔥[NEW!] CrIBo is the first online SSL method that explicitly enforces cross-image consistency at the object/object-part level, showcasing excellent performance on in-context scene understanding across several dense downstream tasks.